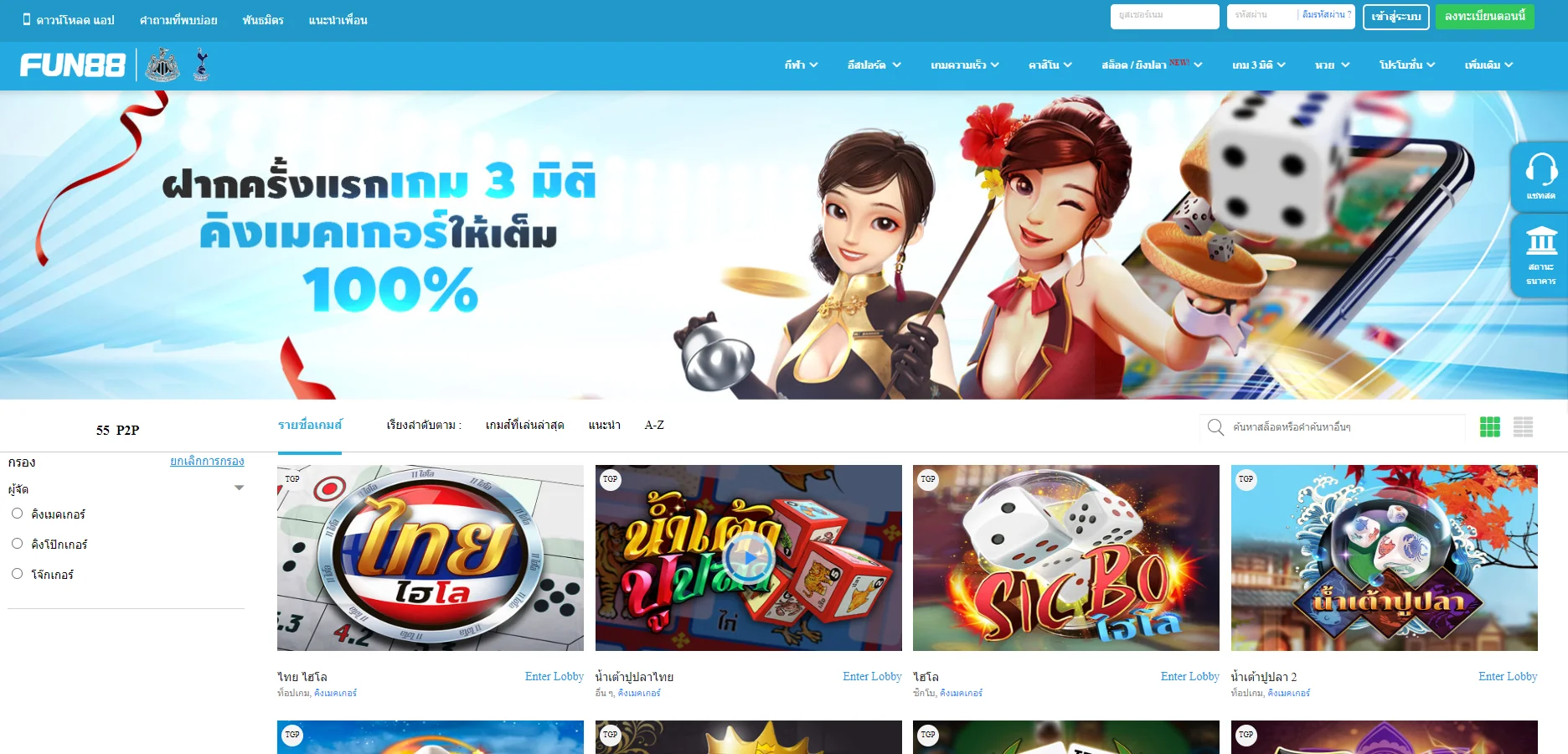
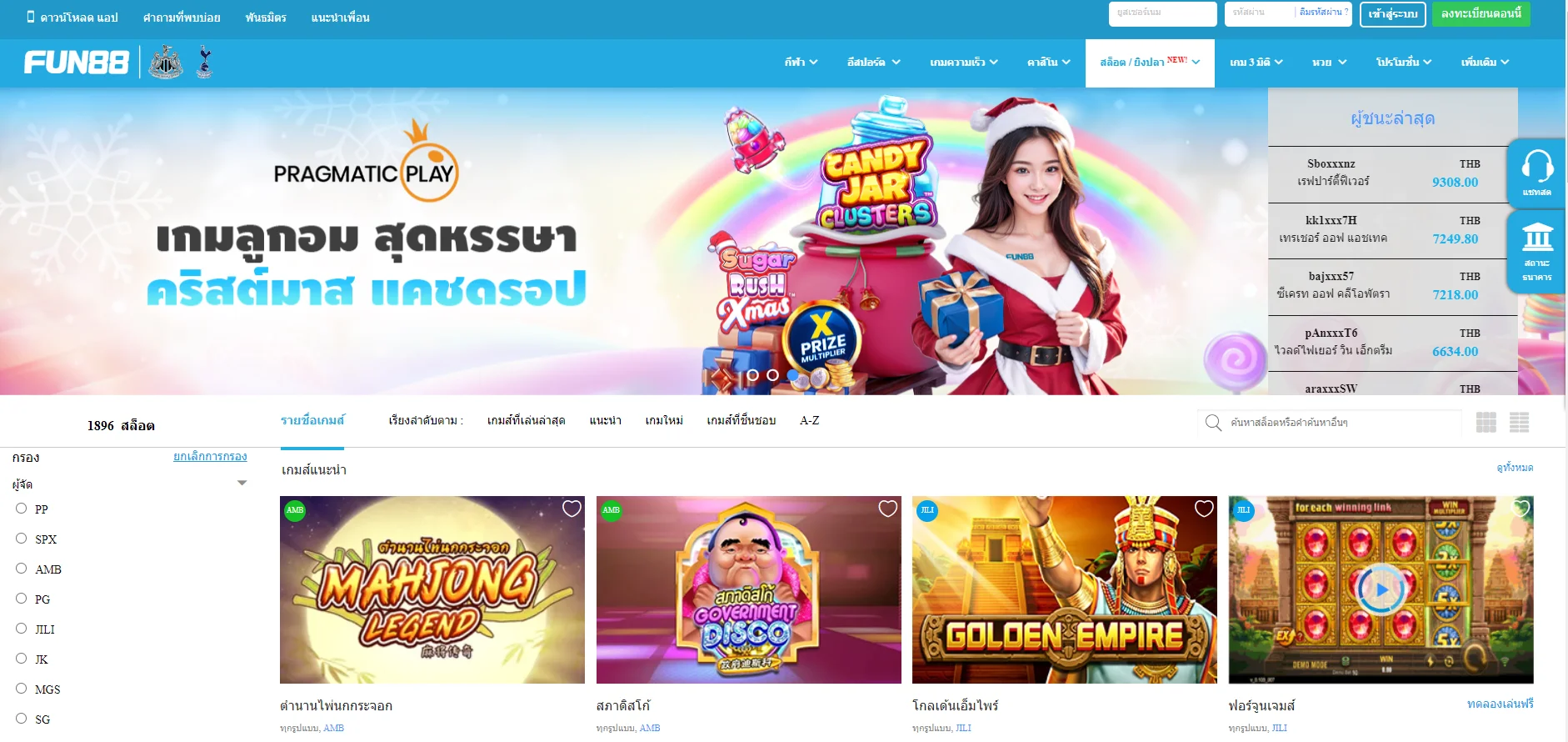
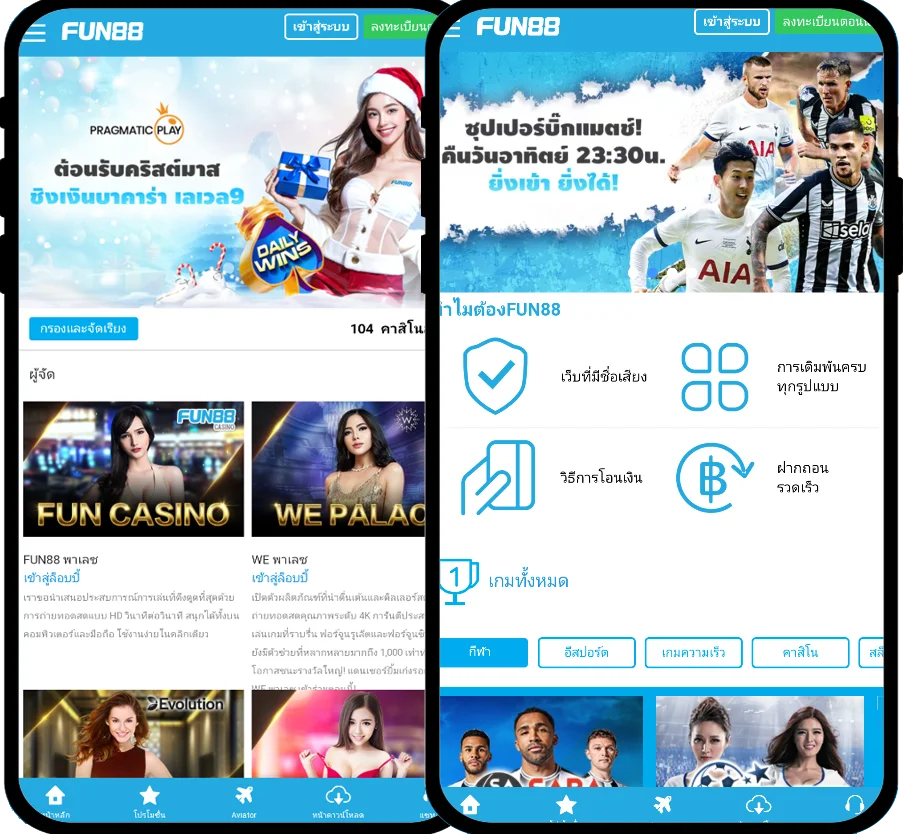
Fun88 ได้รับการประเมินว่าเป็นหนึ่งในเว็บไซต์การพนันออนไลน์ชั้นนำของเอเชียที่ให้บริการเกมหลากหลายและน่าสนใจ รวมถึงการพนันกีฬา คาสิโนออนไลน์ หวย slot และอื่นๆ อีกเยอะ เมื่อมาที่ ฟัน88 ผู้เล่นจะได้สัมผัสกับแพลตฟอร์มที่ทันสมัยโดยมีผลิตภัณฑ์ที่หลากหลาย อัตราการเดิมพันที่ดีที่สุด และโปรโมชั่นที่น่าสนใจมากมาย เข้าชมเว็บหลักของ Fun88.com ผ่าน Fun88 ทางเข้า ล่าสุดที่เราให้มาเพื่อสำรวจโลกของการพนันที่เต็มไปด้วยความมันส์นะคะ
| ✅เจ้าของ: |
💎OG Global Access Limited, E Gambling Montenegro d.o.o. |
| ✅ใบอนุญาต: |
💎PAGCOR, Isle of Man |
| ✅ปีที่ก่อตั้ง: |
💎2008 |
| ✅สำนักงานใหญ่: |
💎Manila - Philippines |
| ✅ทางเข้า Fun88 ล่าสุด 2024 |
💎Fun88.com - ฟัน88 - ฟัน888 - Fun888 - Fan88 |
| ✅ทางเข้า Fun88 มือถือ |
💎m.Fun88 - Fun88 มือถือ - Fun88แท้ - ลิงค์ Fun88 |
| ✅Fun88 เข้าระบบ |
💎Fun88 login - Fun888 เข้าระบบ - Fun88 ล็อกอิน |
| ✅สโมสรและพันธมิตรผู้สนับสนุนก่อนหน้านี้ |
💎La Liga, Burnley FC, Esports OG - Dota 2,... |
| ✅สโมสรและพันธมิตรผู้สนับสนุนปัจจุบัน |
💎Tottenham Hotspur FC, NewCastle United FC |
| ✅แบรนด์แอมบาสเดอร์ของ Fun88 |
- Robbie Fowler (2014-2015)
- Steve Nash (2016-2017)
- Kobe Bryant (2019)
- Iker Casillas (2022)
- Tony Parker (2023)
|
| ✅เกมเดิมพัน |
💎กีฬา, อีสปอร์ต, คาสิโน, สล็อต, เกม 3 มิติ, หวย |
| ✅วิธีการชำระเงิน |
💎โอนเงินผ่านธนาคาร, TrueMoney, EasyPay, Fast Baht,.. |
| ✅ติดต่อ Fun88 Thailand |
|